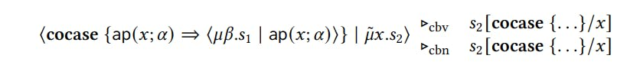Cálculo sequente vs CPS: a perspectiva de um compilador sobre os consumidores e estratégias de avaliação

Tabela de links

1. Introdução
2. Traduzindo -se ao cálculo seqüente

   2.1 Expressões aritméticas

   2.2 Deixe as ligações

   2.3 Definições de nível superior

   2.4 Dados algébricos e tipos de codata

   2.5 Funções de primeira classe

   2.6 Operadores de controle

3. Avaliação dentro de um contexto

   3.1 Contextos de avaliação para diversão

   3.2 foco na avaliação no núcleo

4. Regras de digitação

   4.1 Regras de digitação para diversão

   4.2 Regras de digitação para núcleo

   4.3 Tipo de solidez

5. Percepções

   5.1 Os contextos de avaliação são de primeira classe

   5.2 Os dados são duplos para codata

   5.3 Letrações são duplas para controlar os operadores

   5.4 A transformação de caso de caso

   5.5 Consumidores diretos e indiretos

   5.6 Callg-By-Value, Call-By-Name e Eta-Laws

   5.7 Lógica linear e a dualidade de exceções

6. Trabalho relacionado
7. Conclusão, declaração de disponibilidade de dados e reconhecimentos

A. A relação com o cálculo seqüente

B. Regras de digitação para diversão

C. Semântica operacional da etiqueta/goto

Referências

5.5 Consumidores diretos e indiretos

Conforme mencionado na introdução, um concorrente natural do cálculo seqüente como uma representação intermediária é o estilo de passagem de continuação (CPS). No CPS, os contextos de avaliação reificados são representados por funções. Isso torna os tipos resultantes de programas no CPS, sem dúvida, mais difíceis de entender. Há, no entanto, outra vantagem do cálculo seqüente sobre a CPS, conforme descrito por Downen et al. [2016]. A representação de primeira classe dos consumidores em cálculo seqüente nos permite distinguir entre dois tipos diferentes de consumidores: consumidores diretos, ou seja, destruidores e consumidores indiretos. Em particular, isso permite encadear consumidores diretos em núcleo de maneira semelhante à diversão.

Suponha que tenhamos um tipo de codata com os destruidores obtidos e configurados para obter e definir o valor de uma referência. Agora considere as seguintes chamadas cadeia de destruidores em uma referência 𝑟 em diversão

𝑟 .set (3) .set (4) .get ()

Um compilador pode usar uma regra de reescrita personalizada definida pelo usuário para reescrever duas chamadas subsequentes para definir apenas a segunda chamada. No núcleo, o exemplo acima parece o seguinte:

𝜇𝛼.⟨𝑟 | conjunto (3; conjunto (4; get (𝛼)⟩

Ainda podemos ver imediatamente o encadeamento direto dos destruidores e, assim, aplicar essencialmente a mesma regra de reescrita. No CPS, no entanto, o exemplo prefere se tornar

𝜆𝑘. 𝑟 .set (3; 𝜆𝑠. 𝑠.

O encadeamento dos destruidores fica ofuscado pelas indirições introduzidas, representando as continuações para cada destruidor como uma função. Para aplicar a regra de reescrita personalizada mencionada acima, é necessário ver através dos Lambdas, ou seja, a regra de reescrita personalizada deve ser transformada para ser aplicável.

5.6 Callg-By-Value, Call-By-Name e Eta-Laws

Na Seção 2.2, já apontamos a existência de declarações ⟨𝜇𝛼.𝑠1 | 𝜇𝑥. [𝜇𝑥.𝑠 ˜ 2/𝛼] ou𝑠2 [𝜇𝛼.𝑠1/𝑥]. Esses pares críticos já foram discutidos por Curien e Herbelin [2000] Quando eles introduziram o 𝜆𝜇𝜇 𝜆𝜇𝜇 cálculo. Uma solução é escolher uma ordem de avaliação, chamada por valor (CBV) ou chamada de chamada (CBN), que determina qual das duas declarações devemos avaliar e, neste artigo, escolhemos sempre usar a ordem de avaliação de chamada por valor. A diferença entre essas duas opções também foi discutida por Wadler [2003]. Observe que essa liberdade para a estratégia de avaliação é outra vantagem do cálculo seqüente sobre o estilo de passagem de continuação, pois este sempre conserta uma estratégia de avaliação.

Qual ordem de avaliação escolhemos tem uma consequência importante para as otimizações que podemos executar no compilador. Se escolhermos o valor de chamada por valor, não podemos usar todas as equidades 𝜂 para tipos de codata e, se usarmos o nome de nome, não poderá usar todas as equidades para tipos de dados. Vamos ilustrar o problema no caso de tipos de codata com o exemplo a seguir:

⟨Cocase {AP (𝑥; 𝛼) ⇒ ⟨𝜇𝛽.𝑠1 | AP (𝑥; 𝛼)⟩} | 𝜇𝑥.𝑠 ˜ 2⟩ ≡𝜂 ⟨𝜇𝛽.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩

Assumimos que 𝑥 e 𝛼 não aparecem gratuitamente em 𝑠1. A transformação 𝜂 é apenas a lei comum para funções, mas aplicada à representação de funções como tipos de codata. A declaração no lado esquerdo reduz o 𝜇 𝜇 primeiro em ordem de avaliação de chamada por valor e chamada por nome, ou seja, ou seja,

” alt=”” aria-hidden=”true” />

O lado direito da igualdade 𝜂, no entanto, reduz o 𝜇 primeiro em ordem de avaliação de chamada por valor, ou seja,

Portanto, a igualdade 𝜂 é válida apenas em ordem de avaliação de chamada por nome. Este exemplo mostra que a validade de aplicar esse re-regra como uma otimização depende se o idioma usa o valor de chamada por valor ou o nome. Se usássemos um tipo de dados como par, uma redução semelhante daria apenas o mesmo resultado que a instrução original ao usar o valor chamada.

5.7 Lógica linear e a dualidade de exceções

Introduzimos o par de tipos de dados (𝜎, 𝜏 𝜏) e a lpair do tipo codata (𝜎, 𝜏) como duas maneiras diferentes de formalizar tuplas. O par de tipos de dados (𝜎, 𝜏) é definido pelo TUP do construtor cujos argumentos são avaliados ansiosamente; portanto, esse tipo corresponde a tuplas rigorosas em idiomas como ML ou OCAML. O lpair do tipo codata (𝜎, 𝜏) é um par preguiçoso que é definido por suas duas projeções FST e SND, e somente quando invocamos a primeira ou a segunda projeção, começamos a calcular seu conteúdo. Isso é mais próximo de como as tuplas se comportam em uma linguagem preguiçosa como Haskell.

Lógica linear [Girard 1987; Wadler 1990] Adiciona outra diferença a esses tipos. Na lógica linear, consideramos argumentos como recursos que não podem ser arbitrariamente duplicados ou descartados; Todo argumento para uma função deve ser usado exatamente uma vez. Se seguirmos essa disciplina mais rigorosa, precisamos distinguir entre dois tipos diferentes de pares: para usar um par 𝜎 𝜏 𝜏 (pronunciado “tempos” ou “tensoros”), precisamos usar o 𝜎 e o 𝜏, mas se quisermos usar um par 𝜎 & 𝜏 (pronunciado “com”), devemos escolher o 𝜎 𝜎. Agora é fácil ver que o tipo 𝜎 ⊗ 𝜏 da lógica linear corresponde ao par de tipos de dados (𝜎, 𝜏), pois quando correspondemos a esse tipo nesse tipo, obtemos duas variáveis ​​no contexto, uma para 𝜎 e outra para 𝜏. O tipo 𝜎 & 𝜏 corresponde da mesma forma ao lpair de tipo (𝜎, 𝜏) que usamos invocando a primeira ou a segunda projeção, consumindo o par inteiro.