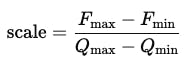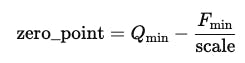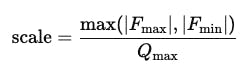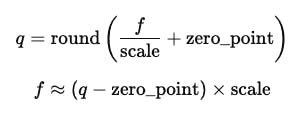A quantização é uma técnica poderosa amplamente utilizada no aprendizado de máquina para reduzir a pegada de memória e os requisitos computacionais das redes neurais, convertendo números de ponto flutuante em números inteiros de precisão mais baixa. Essa abordagem ajuda os modelos a funcionar com eficiência em dispositivos incorporados e {hardware} de borda.
Neste artigo, exploraremos a quantização em detalhes, implementando um processo simples de quantização e desquantização do zero e demonstrará como usá -lo nos modelos Pytorch.
O que é quantização?
A quantização das redes neurais é o processo de converter os pesos e ativações de uma rede neural de formatos de alta precisão (normalmente números de ponto flutuante de 32 bits, ou float32) para formatos de precisão mais baixa (como números inteiros de 8 bits ou Int8).
A principal idéia por trás da quantização é “comprimir” o intervalo de valores possíveis para reduzir o tamanho dos dados e acelerar os cálculos.
As redes neurais estão se tornando maiores e mais complexas, mas seus aplicativos exigem cada vez mais a execução de dispositivos com restrição de recursos, como smartphones, wearables, microcontroladores e dispositivos de borda. A quantização permite:
- Reduzindo o tamanho do modelo: Por exemplo, a mudança do float32 para o INT8 pode encolher um modelo em até 4 vezes.
- Inferência mais rápida: A aritmética inteira é mais rápida e mais eficiente em termos de energia.
- Requisitos de memória inferior e largura de banda: Isso é elementary para dispositivos de borda/IoT e cenários incorporados.
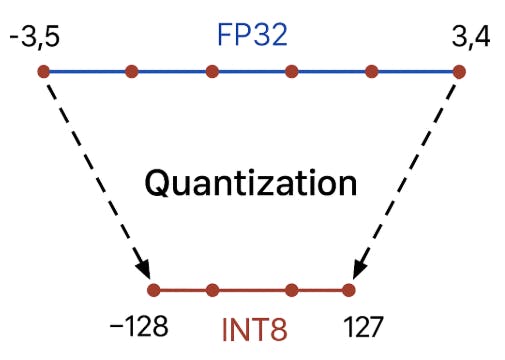
Durante a quantização, os valores de pesos e ativações são mapeados de sua faixa contínua authentic para níveis discretos usando transformações lineares simples.
Por exemplo, o intervalo de valores [-3.5, 3.4] pode ser “cortado” em 256 níveis (INT8) e cada valor actual é arredondado para o nível discreto mais próximo.
Nas redes neurais, a quantização geralmente se refere à conversão de dois tipos de dados: pesos e ativações.
- Pesos são os parâmetros que a rede “lembra” durante o treinamento. Eles determinam o quão fortemente cada entrada afeta a saída de um neurônio. A quantização dos pesos pode reduzir significativamente o tamanho geral do modelo, pois os pesos normalmente ocupam a maior parte da memória.
- As ativações são os valores calculados na saída de cada camada durante a operação da rede (inferência). Essencialmente, esses são os sinais “passados” de uma camada para a próxima. A quantização das ativações é importante para acelerar a inferência, porque a maioria das operações dentro da rede neural é realizada em ativações.
Quantização assimétrica e simétrica
Quando quantizamos valores, precisamos “comprimir” a faixa authentic de números e mapeá -los corretamente entre o Float e o Int.
Isso é alcançado usando dois parâmetros principais escala – Um coeficiente que indica quanto um passo na representação inteira corresponde a uma mudança no valor da flutuação e zero_point – Um valor inteiro que especifica qual valor INT8 corresponde a zero na representação da flutuação.
ondeFmax, Fmin– Os valores de flutuação máxima e mínimaQmax, Qmin – Os valores inteiros máximos e mínimos (127 e -128 para int8)
Existem duas abordagens principais: quantização simétrica e assimétrica. A principal diferença entre a quantização simétrica e assimétrica está na maneira como eles mapeiam os intervalos dos valores originais de flutuação para quantizados inteiros. Com quantização simétrica, a faixa de valor float é sempre centrada em zero (Zero_point é 0); portanto, zero no domínio float corresponde a zero na representação inteira.
Isso simplifica os cálculos e acelera a inferência, mas exige que os valores sejam distribuídos aproximadamente igualmente nos lados positivos e negativos.
Por outro lado, a quantização assimétrica pode funcionar com qualquer intervalo, não necessariamente simétrica, e permite que você mude “zero” para o ponto apropriado. Isso é alcançado usando um ponto zero, que outline qual valor inteiro corresponde a zero na faixa de float. Essa abordagem é especialmente conveniente quando todos os valores em um tensor são positivos ou têm um intervalo fora do padrão, por exemplo, após a aplicação de uma ativação RelU.
Nas redes neurais modernas, os pesos geralmente são quantizados simetricamente, enquanto as ativações são quantizadas assimetricamente, para alcançar o melhor equilíbrio de precisão e desempenho em dispositivos reais.
As fórmulas para quantização e desquantização são as seguintes:
onde
f – o valor authentic da flutuação
q – O valor quantizado
Implementando quantização assimétrica em pytorch
Este exemplo demonstra como implementar manualmente quantização e desquantização assimétrica de um tensor usando pytorch.
Primeiro, um tensor aleatório com valores float32 é gerado
import torch
# Generate a random 2D FP32 tensor (e.g., 4x5)
x_fp32 = torch.randn(4, 5) * 5
print("Unique FP32 tensor:n", x_fp32)
Em seguida, os valores mínimo e máximo desse tensor são calculados, e estes são usados para calcular a escala de parâmetros e zero_point para quantização assimétrica
# Discover min/max for the entire tensor
x_min, x_max = x_fp32.min(), x_fp32.max()
qinfo = torch.iinfo(torch.int8)
qmin, qmax = qinfo.min, qinfo.max
# Calculate scale and zero_point for uneven quantization
scale = (x_max - x_min) / (qmax - qmin)
zero_point = int(torch.spherical(qmin - x_min / scale))
Em seguida, o tensor é convertido no formato inteiro INT8, e os valores são arredondados, escalados e deslocados para caber no intervalo INT8 válido.
# Quantize to INT8
x_q = torch.clamp(torch.spherical(x_fp32 / scale + zero_point), qmin, qmax).to(torch.int8)
print("nQuantized INT8 tensor:n", x_q)
Para fins de teste, os valores quantizados são transformados de volta à faixa Float32 authentic usando a fórmula inversa.
# Dequantize again to FP32
x_dequant = (x_q.float() - zero_point) * scale
print("nDequantized FP32 tensor:n", x_dequant)
Finalmente, os erros de quantização são calculados -Erro ao quadrado da Meia (MSE) e o erro absoluto máximo entre os tensores originais e restaurados.
# Examine: MSE and max absolute error
mse = torch.imply((x_fp32 - x_dequant) ** 2)
max_abs_err = (x_fp32 - x_dequant).abs().max()
print(f"nMSE between authentic and dequantized: {mse:.6f}")
print(f"Max absolute error: {max_abs_err:.6f}")
Este exemplo ilustra claramente como as principais etapas da quantização assimétrica funcionam na prática e que tipos de distorções podem ocorrer ao converter entre representações de flutuação e número inteiro.
Abaixo está a saída da execução do código:
Unique FP32 tensor:
tensor([[ 2.8725, 1.0017, -4.8329, -0.8561, 2.7119],
[ 9.3110, -2.9099, -9.1575, 7.8362, 4.5481],
[-2.4224, 6.4360, 1.0812, -8.9195, 7.3958],
[-1.5830, -1.7517, 4.6271, -9.3345, -9.3382]])
Quantized INT8 tensor:
tensor([[ 39, 14, -66, -12, 37],
[ 127, -40, -125, 107, 62],
[ -33, 88, 15, -122, 101],
[ -22, -24, 63, -128, -128]], dtype=torch.int8)
Dequantized FP32 tensor:
tensor([[ 2.8522, 1.0239, -4.8268, -0.8776, 2.7060],
[ 9.2880, -2.9254, -9.1417, 7.8253, 4.5343],
[-2.4134, 6.4358, 1.0970, -8.9223, 7.3865],
[-1.6089, -1.7552, 4.6074, -9.3611, -9.3611]])
MSE between authentic and dequantized: 0.000275
Max absolute error: 0.026650
Como você pode ver nas métricas calculadas, o erro entre o tensor quantizado e o authentic é muito pequeno e, na maioria dos casos, insignificante para tarefas práticas.
Quantização simétrica pós-treinamento de uma camada linear
Nesta seção, implementamos e testamos uma camada linear simples com quantização simétrica pós-treinamento.
OPTQSymmetricQuantizedLinear A classe se estende nn.Module e imita uma camada padrão totalmente conectada, mas acrescenta a capacidade de quantizar seus pesos após o treinamento usando quantização simétrica de 8 bits.
Após o treinamento, podemos ligar para o quantize_weights() Método, que converte os pesos float32 instruídos em valores de Int8 quantizados e armazenam a escala correspondente. Durante a inferência (ahead), a camada reconstrói os pesos originais de sua representação quantizada e calcula a saída como de costume.
import torch
import torch.nn as nn
import torch.nn.purposeful as F
class PTQSymmetricQuantizedLinear(nn.Module):
def __init__(self, in_features, out_features, bias=True):
tremendous().__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = nn.Parameter(torch.empty(out_features, in_features))
if bias:
self.bias = nn.Parameter(torch.empty(out_features))
else:
self.register_parameter('bias', None)
# buffers for storing quantized weights and scale
self.register_buffer('weight_q', None)
self.register_buffer('weight_scale', None)
@staticmethod
def symmetric_quantize(x):
qmax = 127
max_abs = x.abs().max()
scale = max_abs / qmax if max_abs > 0 else 1.0
x_q = torch.spherical(x / scale).clamp(-qmax, qmax)
return x_q.to(torch.int8), torch.tensor(scale, dtype=torch.float32, system=x.system)
def quantize_weights(self):
w_q, w_scale = self.symmetric_quantize(self.weight.knowledge)
self.weight_q = w_q
self.weight_scale = w_scale
def ahead(self, enter):
weight_deq = self.weight_q.float() * self.weight_scale
return F.linear(enter, weight_deq, self.bias)
Abaixo, mostramos como inicializar a camada, quantizar os pesos, executar a inferência e comparar o resultado quantizado com a saída Float32 authentic. Esse fluxo de trabalho demonstra claramente que a quantização simétrica pode comprimir significativamente o modelo, preservando a maior parte de sua precisão numérica.
layer = PTQSymmetricQuantizedLinear(in_features=4, out_features=3)
# Initialize weights and bias for reproducibility
torch.manual_seed(0)
nn.init.uniform_(layer.weight, -1, 1)
nn.init.uniform_(layer.bias, -0.1, 0.1)
# Generate dummy enter
x = torch.randn(2, 4) # batch_size=2, in_features=4
# Quantize weights
layer.quantize_weights()
# Run ahead go
out = layer(x)
print("Output after quantization:", out)
# Compute the float32 (authentic) layer output
with torch.no_grad():
out_fp = F.linear(x, layer.weight, layer.bias)
print("Output authentic float32:", out_fp)
# Compute the distinction (MSE)
mse = torch.imply((out - out_fp) ** 2)
print("MSE between quantized and float32:", mse.merchandise())
Abaixo está a saída da execução do código:
Output after quantization: tensor([[-0.2760, 0.6149, -0.0378],
[-1.6489, 1.8015, -0.4852]], grad_fn=)
Output authentic float32: tensor([[-0.2753, 0.6172, -0.0395],
[-1.6417, 1.8051, -0.4910]])
MSE between quantized and float32: 1.781566970748827e-05
Conclusão
A quantização é uma tecnologia-chave que permite que as redes neurais modernas sejam executadas não apenas em servidores poderosos, mas também em dispositivos com restrição de recursos, como smartphones, wearables, microcontroladores e dispositivos de borda. Ao converter pesos e ativações do float32 para o formato INT8 mais compacto, os modelos se tornam significativamente menores, requerem menos memória e computação e os tempos de inferência são visivelmente reduzidos.
Neste artigo, exploramos como a quantização funciona, discutimos as diferenças entre abordagens simétricas e assimétricas e implementamos exemplos básicos dessas técnicas em Pytorch, desde os tensores quantizados manualmente até a quantização pós-treinamento de camadas de rede neural.
Experimente você mesmo no github
Se você deseja explorar esses exemplos, sinta-se à vontade para visitar meu repositório do GitHub, onde encontrará todos os arquivos de origem para o código neste artigo. Você pode clonar o repositório, abrir o código no seu sistema de construção ou sistema de construção favorito e experimentar. Aproveite brincar com os exemplos!
Me siga
Github